60. Sudoku

Task

Sudoku is a number-placement puzzle. The objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 sub-grids that compose the grid contains all of the digits from 1 to 9.

This algorithm should check if the given grid of numbers represents a correct solution to Sudoku.

Example

• For

  grid = [[1, 3, 2, 5, 4, 6, 9, 8, 7],
          [4, 6, 5, 8, 7, 9, 3, 2, 1],
          [7, 9, 8, 2, 1, 3, 6, 5, 4],
          [9, 2, 1, 4, 3, 5, 8, 7, 6],
          [3, 5, 4, 7, 6, 8, 2, 1, 9],
          [6, 8, 7, 1, 9, 2, 5, 4, 3],
          [5, 7, 6, 9, 8, 1, 4, 3, 2],
          [2, 4, 3, 6, 5, 7, 1, 9, 8],
          [8, 1, 9, 3, 2, 4, 7, 6, 5]]
  

  the output should be
  sudoku(grid) = true;

• For

  grid = [[1, 3, 2, 5, 4, 6, 9, 2, 7],
          [4, 6, 5, 8, 7, 9, 3, 8, 1],
          [7, 9, 8, 2, 1, 3, 6, 5, 4],
          [9, 2, 1, 4, 3, 5, 8, 7, 6],
          [3, 5, 4, 7, 6, 8, 2, 1, 9],
          [6, 8, 7, 1, 9, 2, 5, 4, 3],
          [5, 7, 6, 9, 8, 1, 4, 3, 2],
          [2, 4, 3, 6, 5, 7, 1, 9, 8],
          [8, 1, 9, 3, 2, 4, 7, 6, 5]]
  

  the output should be
  sudoku(grid) = false.
  
  The output should be false: each of the nine 3 × 3 sub-grids should contain all of the digits from 1 to 9.
  These examples are represented on the image below.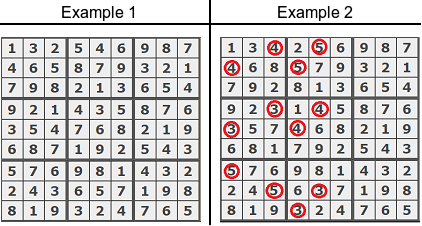

Input/Output

• [execution time limit]
  4 seconds (py3)

• [input] array.array.integer grid
  A matrix representing 9 × 9 grid already filled with numbers from 1 to 9.
  Guaranteed constraints: grid.length = 9, grid[i].length = 9, 1 ≤ grid[i][j] ≤ 9.

• [output] boolean
  true if the given grid represents a correct solution to Sudoku, false otherwise.

My Solution

def sudoku(grid):
    rowTrue = all([set(grid[row]) == set(range(1, 10)) for row in range(9)])
    columnTrue = all([set([grid[row][column] for row in range(9)]) == set(range(1, 10))
                      for column in range(9)])
    subGridTrue = True
    for column in range(3):
        for i in range(3):
            subGrid = set()
            for row in range(3 * i, 3 * (i + 1)):
                for j in range(3):
                    subGrid.add(grid[row][3 * column + j])
            if subGrid != set(range(1, 10)):
                subGridTrue = False
    return rowTrue and columnTrue and subGridTrue